Del Mar Photonics - SAM basics - SAM FAQ - SAM brochure

Resonant saturable absorber mirror RSAM-1064-25.4s

Del Mar Photonics RSAM-1064-25.4s resonant saturable absorber mirror, λ = 1064 nm, modulation depth ΔR = 90 %, low intensity reflectance < 1%, FWHM = 25 nm, relaxation time τ ~ 9 ps chip size: 4mm x 4mm, soldered on the center of a gold-plated Cu-cylinder with 25.4 mm

RSAM-1064-25.4s resonant saturable absorber mirror, λ = 1064 nm, modulation depth ΔR = 90 %, low intensity reflectance < 1%, FWHM = 25 nm, relaxation time τ ~ 9 ps chip size: 4mm x 4mm, soldered on the center of a gold-plated Cu-cylinder with 25.4 mm.

RSAM - Resonant Saturable Absorber Mirror

 
  >  Contents  
   
>  How does a RSAM work?  
 

The resonant saturable absorber mirror (RSAM) is a similar device as a saturable absorber mirror (SAM), but has a larger saturable absorption, a smaller bandwidth and a lower saturation fluence. The RSAM is designed as a resonant Gires傍ournois interferometer with absorber layers positioned at the antinodes of the optical field inside the resonator cavity. The resonant saturable absorber mirror (RSAM) is a similar device as a saturable absorber mirror (SAM), but has a larger saturable absorption, a smaller bandwidth and a lower saturation fluence. The RSAM is designed as a resonant Gires傍ournois interferometer with absorber layers positioned at the antinodes of the optical field inside the resonator cavity.

The RSAM is a nonlinear optical device, having a low reflectance for week optical signals like noise and a high reflectance for high power signals like optical pulses. Optical pulses saturate the absorber material inside the resonant cavity of the RSAM. Due to the short recovery time of the absorber material the RSAM blocks immediately after the reflected pulse the optical noise floor.

Important parameters of the RSAM are the

down
 
>  RSAM applications  
  The main applications for RSAMs are:
  • optical noise suppression, for example after an EDFA or a pulse picker (unsaturated RSAM reflectance = 0) --> SANOS (SAturable NOise Suppressor)
  • opto-optical wavelength conversion (unsaturated RSAM reflectance = 0)
  • passive mode-locking of fiber lasers (unsaturated RSAM reflectance > 0).
 
 
>  Resonance wavelength  
  Influence of the angle of incidence  
  The resonance wavelength l of the Gires傍ournois interferometer depends on the angle of incidence j and is given by  
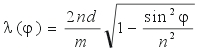
  Formula lambda eq.(1)  
  with  
  l resonance wavelength of the interferometer  
  n refractive index of the absorbing spacer layer up
  d thickness of the absorbing spacer layer  
  m order of the resonance; m = 1, 2, 3, ....  
  j angle of incidence on the RSAM  
 
  In case of a perpendicular beam incidence the first order resonance wavelength is simply l = 2nd. down
 
  Angle of incidence Resonance wavelength l of a RSAM
with l(0) = 1064 nm and n = 3.1 after eq. (1)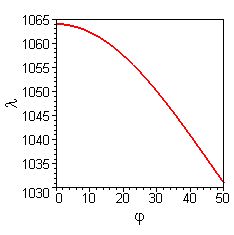
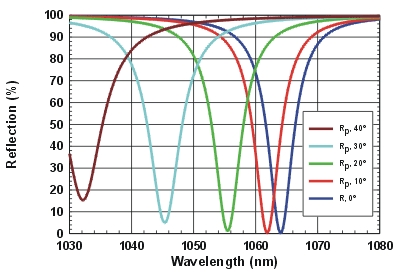
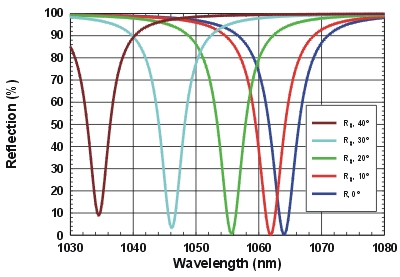
Resonance wavelength as a function of incidence angle 		 
  Del Mar Photonics RSAM: Resonance wavelength for parallel polarized light at different angles of incidence Resonance wavelength for parallel polarized light at different angles of incidence  
  Del Mar Photonics RSAM: Resonance wavelength for perpendicular polarized light at different angles of incidence Resonance wavelength for perpendicular polarized light at different angles of incidence  
 
  Influence of the temperature  
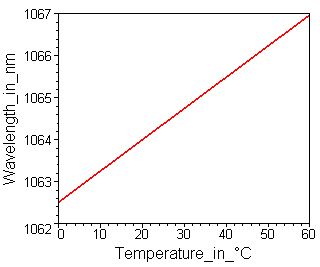
  There is also a temperature influence on the resonance wavelength l. The temperature dependency of the optical thickness nd of the absorbing spacer layer, which governs the resonance wavelength l, is mainly determined by the refractive index. The influence of the thermal expansion of the layer thickness is negligible.  
  The change of the resonance wavelength l with the temperature can be calculated by  
 
  formula lambda (T) eq.(2)  
 
  with  
  l (T) resonance wavelength at temperature T  
  l (T0) resonance wavelength at reference temperature T0  
  1/n*dn/dT ~ 7.5x10-5K-1, temperature coefficient of the refractive index  
  T0 reference temperature  
  T working temperature  
 
  RSAM: Temperature dependency of the resonance wavelength Resonance wavelength l of a RSAM with l(0) = 1064 nm after eq. (2)
 		  
 
 
>  Bandwidth  
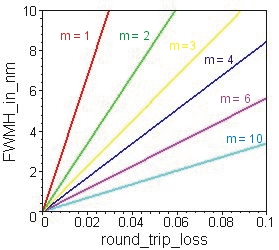
  The bandwidth Dl of the interferometer resonance dip is gouverned by the round trip loss l of the wave inside the cavity and can be estimated in case of small losses l << 1 by  
 
  Dl = l (1 - rf + A)/(m π) = ll/(m π)  
 
  with  
  Dl bandwidth FWHM (full width at half maximum)  
  l resonance wavelength of the interferometer  
  (rf)2 = Rf reflectance of the front mirror (back mirror reflectance Rb = 1)  
  A single pass absorptance of the spacer layer  
  m order of the resonance; m = 1, 2, 3, ....  
  l round trip loss: 1 - rf + A up
 
  Dl for RSAM
at l = 1064 nm 		RSAM: FWMH as a function of the round trip loss 1-Rf-2A down
 
 
  RSAM, impedance matched at l = 1064 nm with front mirror reflection rf = 0.97,
unsaturated absorption of A = 1.5% and resonance order m = 4
Del Mar Photonics RSAM: Reflectance as a function of absorption A 		down
up
 
 
>  Saturation intensity  
  The RSAM is a strong nonlinear optical device. The absorptance A of the absorber layer and the reflectance R of the RSAM depend on the incoming light intensity I. Due to the resonance condition of the Gires傍ournois interferometer at the working wavelength the effective saturation intensity Isat,eff of the device shifts by a factor of about (p/F)2 (F - finesse of the Gires傍ournois interferometer) to lower values in relation to the intrinsic material value Isat, which is valid for non-resonant saturable absorber mirrors (SAM).
The absorptance A of a RSAM with a not too small finesse F > 10 can be estimated by 		 
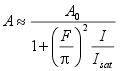
  Formula absorption eq.(3) down
  with  
  A absorptance  
  A0 small signal absorptance (saturable absorption)  
  I light intensity (measured in W/m2)  
  Isat intrinsic material saturation intensity  
  F finesse of the RSAM  
 
  The effective saturation fluence Fsat,eff  of a RSAM can be estimated using the relaxation time t and the effective saturation intensity Isat,eff  
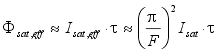
  Formula absorption eq.(4)  
  with  
  Fsat,eff effective saturation fluence of the RSAM  
  Isat,eff effective saturation intensity of the RSAM  
  t relaxation time of the absorber material  
 
  With typical values for a non-resonant SAM
  •  Isat = 10 MW/cm2
  •    t = 10 ps
  • Fsat = 100 mJ/cm2

the relevant parameters for a RSAM with a finesse F = 20 can be estimated to

  •  Isat,eff = 250 kW/cm2
  • Fsat,eff = 2.5 mJ/cm2

In this way the effective saturation values can be decreased to very low values at the expense of a small usuable spectral bandwidth.

 
 
 
>  Intensity dependent reflectance  
  RSAM at l = 1064 nm with front mirror reflection rf = 0.97,
unsaturated absorption of A = 1.5% and resonance order m = 4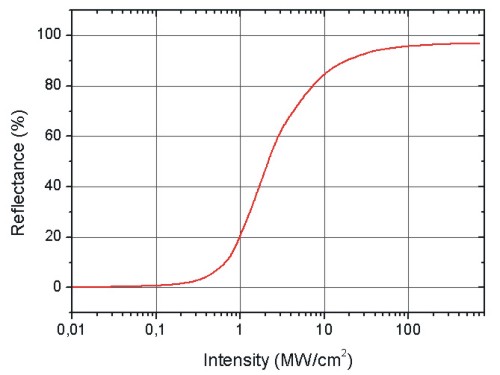
Reflectance as a function of input intensity I 		down
up
 
 
>  Relaxation time  
 

The saturable absorber layer consists of a semiconductor material with a direct band gap, which is slightly smaller than the photon energy. During the absorption electron-hole pairs are created in the film. The relaxation time t of the carriers is very short due to fast non-radiative relaxation channels introduced by low-temperature growth of the absorber layer.

Typical values of the relaxation time t are between 5 and 20 ps.

The relaxation of the carriers and the recovery of the absorption A(t) after the saturation can be described as

 Recovery of the absorption A0
with a relaxation time t = 10 ps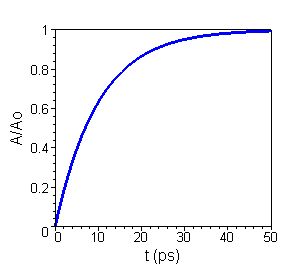
relaxation 		up
 
  A(t) = A0[1 - exp(-t/t )]  
 
  with    
 
  A(t) time dependent absorption  
  A0 small signal saturable absorption  
  t time  
  t relaxation time  
 
 

 

SAM basics - SAM FAQ - SAM brochure

 

1064 nm
 
Saturable Absorber Mirror Working wavelength 1064 nm (1020-1110 nm) Saturable absorptance 0.5%, 1%, 2%, 3%, 4%, 5%, 6%, 8%, 10%, 12%, 13%, 27%, 30%, 45%, or 70%
 Model   Product Name+   Price   Buy Now 
 SAM-1064-2-0   SAM 1064 nm, absorptance 2%, 1x1 mm or 1.3x1.3 mm, thck. 400 ｵm   $575.00  Buy Now 
 SAM-1064-2-0   SAM 1064 nm, absorptance 2%, 4x4 mm, thickness 400 ｵm   $575.00  Buy Now 
 SAM-1064-2-FC/PC   SAM 1064 nm, absorptance 2%, mounted: cable   $811.00  Buy Now 
 SAM-1064-2-12.7g   SAM 1064 nm, absorptance 2%, mounted: glued   $676.00  Buy Now 
 SAM-1064-2-25.0g   SAM 1064 nm, absorptance 2%, mounted: glued   $676.00  Buy Now 
 SAM-1064-2-25.4g   SAM 1064 nm, absorptance 2%, mounted: glued   $676.00  Buy Now 
 SAM-1064-2-12.7s   SAM 1064 nm, absorptance 2%, mounted: soldered   $727.00  Buy Now 
 SAM-1064-2-25.0s   SAM 1064 nm, absorptance 2%, mounted: soldered   $727.00  Buy Now 
 SAM-1064-2-25.4s   SAM 1064 nm, absorptance 2%, mounted: soldered   $727.00  Buy Now 

more